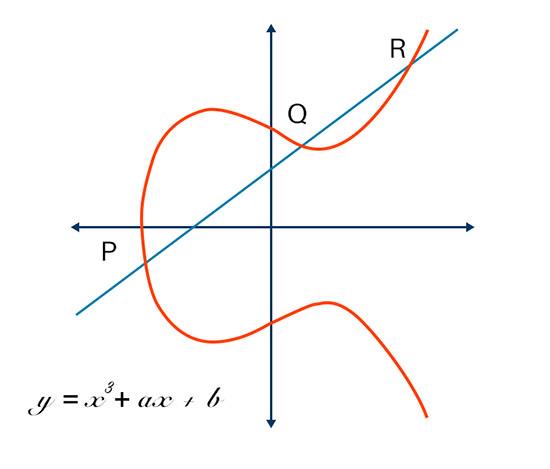Что такое криптография эллиптических кривых (ECC)?

Криптография на основе эллиптических кривых (ECC) — это метод криптографии с открытым ключом, основанный на теории эллиптических кривых, помогающий создавать более быструю, компактную и надежную криптографию. ECC генерирует шифры на основе свойств уравнений эллиптических кривых вместо традиционного метода использования больших простых чисел. Эту технологию можно использовать в сочетании с большинством общедоступных методов шифрования , таких как RSA и Diffie-Hellman.

По мнению некоторых исследователей, ECC достигает такого уровня безопасности всего за 164 бита, в то время как другим системам для достижения того же уровня требуется 1024 бита. Поскольку ECC помогает обеспечить безопасность при низком расходе вычислительной мощности и заряда аккумулятора, он широко применяется в мобильных приложениях.

ECC был разработан компанией Certicom, поставщиком систем безопасности мобильного электронного бизнеса, и недавно получил лицензию от Hifn, производителя интегральных схем и продуктов кибербезопасности. RSA также в настоящее время разрабатывает собственный ECC. Многие компании, включая 3COM, Cylink, Motorola, Pitney Bowes, Siemens, TRW и VeriFone, поддерживают ECC в своих продуктах.

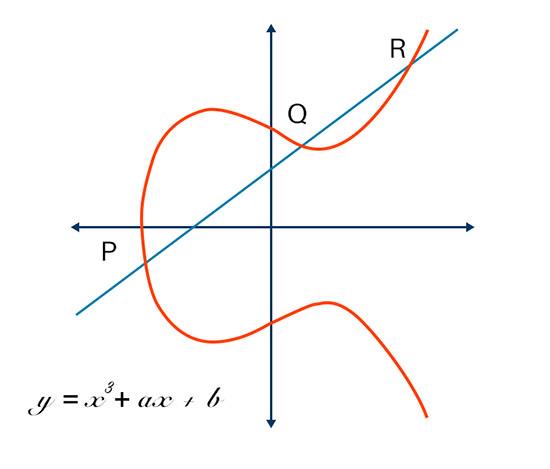
Уравнение и график эллиптической кривой

Свойства и функции эллиптических кривых изучаются математикой уже 150 лет. Их использование в качестве криптографии было впервые предложено в 1985 году Нилом Коблицем из Вашингтонского университета и Виктором Миллером из IBM (это два независимых исследования).

Эллиптическая кривая не является эллипсом (овалом), а изображается в виде круга, пересекающего две оси. ECC основан на свойствах уравнения определенного типа, созданного из группы (набора элементов с бинарной операцией, объединяющей любые два элемента набора в третий элемент). График формируется из точек пересечения кривой и двух осей. Умножьте эту точку на число, чтобы найти следующую точку, но трудно понять, на какое число умножать, даже если результат и следующая точка уже заданы.

Уравнения эллиптических кривых обладают свойством чрезвычайно ценным для криптографических целей, поскольку их легко реализовать, но чрезвычайно сложно обратить.

Однако использование эллиптических кривых все еще имеет некоторые ограничения в этой отрасли. Найджел Смарт, исследователь из Hewlett Packard, обнаружил в этой кривой несколько недостатков, из-за которых ее очень легко взломать. Однако, по словам Филипа Дека из Certicom, хотя эти кривые уязвимы, разработчики ECC знают, как их классифицировать для использования. Он считает, что ECC — это уникальная технология, которую можно использовать во всем мире и на всех устройствах. По словам Дека, «единственное, что делает это, — это эллиптическая кривая».